ELETROMAGNETISMO
Determine o gradiente da função f(x,y,z) = ln(x2 + y2 +z2 ) no ponto P(1,1,-1)
( 4/ 3 , 4/ 3 ,- 2/ 3 )
( 7/ 3 , 8/ 3 ,- 2/ 3 )
( 2/ 3 , 2/ 3 ,- 2/ 3 )
( 2 , 2 ,- 2 )
( 3 , 3 ,- 3 )
Calcule aproximadamente a intensidade da força elétrica resultante sobre uma particula Q1 = 3x10- 4 C está colocada no ponto P1(1,2,3) m. Uma outra particula Q2 = -10- 4 C que está colocada no ponto P2(2,0,5) m. Considere a constante eletrostática igual a  N.m²/c².
N.m²/c².
F =20(6i -2j + 2k)
F =20(5i -2j + 5k)
F =10(1i -2j + 2k)
F =10(9i -4j + 2k)
F =10(3i -2j + 3k)
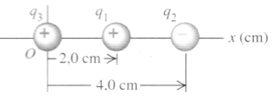
Qual é aproximadamente o módulo da força resultante exercida por essas duas partículas, q1 e q2 sobre uma partícula q3 = 5nC localizada na origem, sabendo que q1 = 1 nC e q2 = - 3 nC, Considere a constante eletrostática igual a 9.109 N.m2/C2
12,8 x 10-4N
7 x 106 N
2,8 x 10-5 N
4 x 104 N
8 x 10-6 N
No campo vetorial abaixo calcule o rotacional:
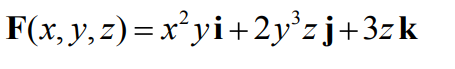
-2y3i -x2k
-8y2i -x3k
-9y2i -x7k
-4y5i -xk
-5y3i -x3k
Sendo u = ( 2,3,1) e v = ( 1,4, 5) . Calcular o vetor W = u · v
W = ( 4,5,5)
W = ( 12,12,15)
W = ( 3,2,5)
W = ( 2,12,5)
W = (12,12,5)
Três partículas com cargas iguais a q1 = 4,9.10-3 C , q2 = − 2,5. 10-3 C e q3 = 0,6. 10-3 C estão situadas nos vértices de um triângulo equilátero, cujo lado vale 3 mm.
Determine aproximidamente para essa situação a energia potencial elétrica do sistema, considere a constante eletrostática igual a 9.109 N.m2/C2
9000 J
5000 J
7800 J
4000 J
3200 J
Uma força de 2,2.10-3 N atua sobre um condutor de 25 cm de comprimento de um fio portador de corrente que é perpendicular a um campo magnético de 340.10-3 T, determine aproximadamente a intensidade da corrente elétrica em A que percorre o fio.
0,8
0,5
0,026
1,2
0,3
Calcule aproximadamente a força elétrica em N, exercida entre duas pequenas esferas condutoras idênticas que são colocadas com seus centros separados por 0,3m. Sendo uma partícula eletrizada com carga de 12 nC, e a outra com uma carga de 18 nC. Considere a constante eletrostática igual a 9.109 N.m²/c².
16.10⁻5
1,6.10⁻5

8.10⁻5
2,16.10⁻5
Utilizando a lei de Ampere, Calcule aproximadamente o campo magnético no centro de um solenóide de. 0,1m de comprimento, com 600 espiras e percorrido por uma corrente de 2 A. Considere a permeabilidade igual a 
( 4/ 3 , 4/ 3 ,- 2/ 3 )
( 7/ 3 , 8/ 3 ,- 2/ 3 )
( 2/ 3 , 2/ 3 ,- 2/ 3 )
( 2 , 2 ,- 2 )
( 3 , 3 ,- 3 )
Calcule aproximadamente a intensidade da força elétrica resultante sobre uma particula Q1 = 3x10- 4 C está colocada no ponto P1(1,2,3) m. Uma outra particula Q2 = -10- 4 C que está colocada no ponto P2(2,0,5) m. Considere a constante eletrostática igual a  N.m²/c².
N.m²/c².
F =20(6i -2j + 2k)
F =20(5i -2j + 5k)
F =10(1i -2j + 2k)
F =10(9i -4j + 2k)
F =10(3i -2j + 3k)
Qual é aproximadamente o módulo da força resultante exercida por essas duas partículas, q1 e q2 sobre uma partícula q3 = 5nC localizada na origem, sabendo que q1 = 1 nC e q2 = - 3 nC, Considere a constante eletrostática igual a 9.109 N.m2/C2

12,8 x 10-4N
7 x 106 N
2,8 x 10-5 N
4 x 104 N
8 x 10-6 N
No campo vetorial abaixo calcule o rotacional:
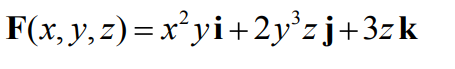
-2y3i -x2k
-8y2i -x3k
-9y2i -x7k
-4y5i -xk
-5y3i -x3k
Sendo u = ( 2,3,1) e v = ( 1,4, 5) . Calcular o vetor W = u · v
W = ( 4,5,5)
W = ( 12,12,15)
W = ( 3,2,5)
W = ( 2,12,5)
W = (12,12,5)
Três partículas com cargas iguais a q1 = 4,9.10-3 C , q2 = − 2,5. 10-3 C e q3 = 0,6. 10-3 C estão situadas nos vértices de um triângulo equilátero, cujo lado vale 3 mm.
Determine aproximidamente para essa situação a energia potencial elétrica do sistema, considere a constante eletrostática igual a 9.109 N.m2/C2
9000 J
5000 J
7800 J
4000 J
3200 J
Uma força de 2,2.10-3 N atua sobre um condutor de 25 cm de comprimento de um fio portador de corrente que é perpendicular a um campo magnético de 340.10-3 T, determine aproximadamente a intensidade da corrente elétrica em A que percorre o fio.
0,8
0,5
0,026
1,2
0,3
Calcule aproximadamente a força elétrica em N, exercida entre duas pequenas esferas condutoras idênticas que são colocadas com seus centros separados por 0,3m. Sendo uma partícula eletrizada com carga de 12 nC, e a outra com uma carga de 18 nC. Considere a constante eletrostática igual a 9.109 N.m²/c².
16.10⁻5
1,6.10⁻5

8.10⁻5
2,16.10⁻5
Utilizando a lei de Ampere, Calcule aproximadamente o campo magnético no centro de um solenóide de. 0,1m de comprimento, com 600 espiras e percorrido por uma corrente de 2 A. Considere a permeabilidade igual a 
F =20(6i -2j + 2k)
F =20(5i -2j + 5k)
F =10(1i -2j + 2k)
F =10(9i -4j + 2k)
F =10(3i -2j + 3k)
Qual é aproximadamente o módulo da força resultante exercida por essas duas partículas, q1 e q2 sobre uma partícula q3 = 5nC localizada na origem, sabendo que q1 = 1 nC e q2 = - 3 nC, Considere a constante eletrostática igual a 9.109 N.m2/C2

12,8 x 10-4N
7 x 106 N
2,8 x 10-5 N
4 x 104 N
8 x 10-6 N
No campo vetorial abaixo calcule o rotacional:
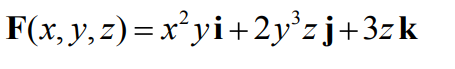
-2y3i -x2k
-8y2i -x3k
-9y2i -x7k
-4y5i -xk
-5y3i -x3k
Sendo u = ( 2,3,1) e v = ( 1,4, 5) . Calcular o vetor W = u · v
W = ( 4,5,5)
W = ( 12,12,15)
W = ( 3,2,5)
W = ( 2,12,5)
W = (12,12,5)
Três partículas com cargas iguais a q1 = 4,9.10-3 C , q2 = − 2,5. 10-3 C e q3 = 0,6. 10-3 C estão situadas nos vértices de um triângulo equilátero, cujo lado vale 3 mm.
Determine aproximidamente para essa situação a energia potencial elétrica do sistema, considere a constante eletrostática igual a 9.109 N.m2/C2
9000 J
5000 J
7800 J
4000 J
3200 J
Uma força de 2,2.10-3 N atua sobre um condutor de 25 cm de comprimento de um fio portador de corrente que é perpendicular a um campo magnético de 340.10-3 T, determine aproximadamente a intensidade da corrente elétrica em A que percorre o fio.
0,8
0,5
0,026
1,2
0,3
Calcule aproximadamente a força elétrica em N, exercida entre duas pequenas esferas condutoras idênticas que são colocadas com seus centros separados por 0,3m. Sendo uma partícula eletrizada com carga de 12 nC, e a outra com uma carga de 18 nC. Considere a constante eletrostática igual a 9.109 N.m²/c².
16.10⁻5
1,6.10⁻5

8.10⁻5
2,16.10⁻5
Utilizando a lei de Ampere, Calcule aproximadamente o campo magnético no centro de um solenóide de. 0,1m de comprimento, com 600 espiras e percorrido por uma corrente de 2 A. Considere a permeabilidade igual a 

12,8 x 10-4N
7 x 106 N
2,8 x 10-5 N
4 x 104 N
8 x 10-6 N
No campo vetorial abaixo calcule o rotacional:
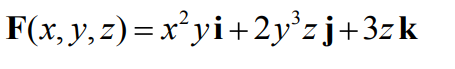
-2y3i -x2k
-8y2i -x3k
-9y2i -x7k
-4y5i -xk
-5y3i -x3k
Sendo u = ( 2,3,1) e v = ( 1,4, 5) . Calcular o vetor W = u · v
W = ( 4,5,5)
W = ( 12,12,15)
W = ( 3,2,5)
W = ( 2,12,5)
W = (12,12,5)
Três partículas com cargas iguais a q1 = 4,9.10-3 C , q2 = − 2,5. 10-3 C e q3 = 0,6. 10-3 C estão situadas nos vértices de um triângulo equilátero, cujo lado vale 3 mm.
Determine aproximidamente para essa situação a energia potencial elétrica do sistema, considere a constante eletrostática igual a 9.109 N.m2/C2
9000 J
5000 J
7800 J
4000 J
3200 J
Uma força de 2,2.10-3 N atua sobre um condutor de 25 cm de comprimento de um fio portador de corrente que é perpendicular a um campo magnético de 340.10-3 T, determine aproximadamente a intensidade da corrente elétrica em A que percorre o fio.
0,8
0,5
0,026
1,2
0,3
Calcule aproximadamente a força elétrica em N, exercida entre duas pequenas esferas condutoras idênticas que são colocadas com seus centros separados por 0,3m. Sendo uma partícula eletrizada com carga de 12 nC, e a outra com uma carga de 18 nC. Considere a constante eletrostática igual a 9.109 N.m²/c².
16.10⁻5
1,6.10⁻5

8.10⁻5
2,16.10⁻5
Utilizando a lei de Ampere, Calcule aproximadamente o campo magnético no centro de um solenóide de. 0,1m de comprimento, com 600 espiras e percorrido por uma corrente de 2 A. Considere a permeabilidade igual a 
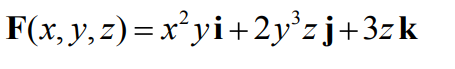
-2y3i -x2k
-8y2i -x3k
-9y2i -x7k
-4y5i -xk
-5y3i -x3k
Sendo u = ( 2,3,1) e v = ( 1,4, 5) . Calcular o vetor W = u · v
W = ( 4,5,5)
W = ( 12,12,15)
W = ( 3,2,5)
W = ( 2,12,5)
W = (12,12,5)
Três partículas com cargas iguais a q1 = 4,9.10-3 C , q2 = − 2,5. 10-3 C e q3 = 0,6. 10-3 C estão situadas nos vértices de um triângulo equilátero, cujo lado vale 3 mm.
Determine aproximidamente para essa situação a energia potencial elétrica do sistema, considere a constante eletrostática igual a 9.109 N.m2/C2
9000 J
5000 J
7800 J
4000 J
3200 J
Uma força de 2,2.10-3 N atua sobre um condutor de 25 cm de comprimento de um fio portador de corrente que é perpendicular a um campo magnético de 340.10-3 T, determine aproximadamente a intensidade da corrente elétrica em A que percorre o fio.
0,8
0,5
0,026
1,2
0,3
Calcule aproximadamente a força elétrica em N, exercida entre duas pequenas esferas condutoras idênticas que são colocadas com seus centros separados por 0,3m. Sendo uma partícula eletrizada com carga de 12 nC, e a outra com uma carga de 18 nC. Considere a constante eletrostática igual a 9.109 N.m²/c².
16.10⁻5
1,6.10⁻5

8.10⁻5
2,16.10⁻5
Utilizando a lei de Ampere, Calcule aproximadamente o campo magnético no centro de um solenóide de. 0,1m de comprimento, com 600 espiras e percorrido por uma corrente de 2 A. Considere a permeabilidade igual a 
W = ( 4,5,5)
W = ( 12,12,15)
W = ( 3,2,5)
W = ( 2,12,5)
W = (12,12,5)
Três partículas com cargas iguais a q1 = 4,9.10-3 C , q2 = − 2,5. 10-3 C e q3 = 0,6. 10-3 C estão situadas nos vértices de um triângulo equilátero, cujo lado vale 3 mm.
Determine aproximidamente para essa situação a energia potencial elétrica do sistema, considere a constante eletrostática igual a 9.109 N.m2/C2
9000 J
5000 J
7800 J
4000 J
3200 J
Uma força de 2,2.10-3 N atua sobre um condutor de 25 cm de comprimento de um fio portador de corrente que é perpendicular a um campo magnético de 340.10-3 T, determine aproximadamente a intensidade da corrente elétrica em A que percorre o fio.
0,8
0,5
0,026
1,2
0,3
Calcule aproximadamente a força elétrica em N, exercida entre duas pequenas esferas condutoras idênticas que são colocadas com seus centros separados por 0,3m. Sendo uma partícula eletrizada com carga de 12 nC, e a outra com uma carga de 18 nC. Considere a constante eletrostática igual a 9.109 N.m²/c².
16.10⁻5
1,6.10⁻5

8.10⁻5
2,16.10⁻5
Utilizando a lei de Ampere, Calcule aproximadamente o campo magnético no centro de um solenóide de. 0,1m de comprimento, com 600 espiras e percorrido por uma corrente de 2 A. Considere a permeabilidade igual a 
9000 J
5000 J
7800 J
4000 J
3200 J
Uma força de 2,2.10-3 N atua sobre um condutor de 25 cm de comprimento de um fio portador de corrente que é perpendicular a um campo magnético de 340.10-3 T, determine aproximadamente a intensidade da corrente elétrica em A que percorre o fio.
0,8
0,5
0,026
1,2
0,3
Calcule aproximadamente a força elétrica em N, exercida entre duas pequenas esferas condutoras idênticas que são colocadas com seus centros separados por 0,3m. Sendo uma partícula eletrizada com carga de 12 nC, e a outra com uma carga de 18 nC. Considere a constante eletrostática igual a 9.109 N.m²/c².
16.10⁻5
1,6.10⁻5

8.10⁻5
2,16.10⁻5
Utilizando a lei de Ampere, Calcule aproximadamente o campo magnético no centro de um solenóide de. 0,1m de comprimento, com 600 espiras e percorrido por uma corrente de 2 A. Considere a permeabilidade igual a 
0,8
0,5
0,026
1,2
0,3
Calcule aproximadamente a força elétrica em N, exercida entre duas pequenas esferas condutoras idênticas que são colocadas com seus centros separados por 0,3m. Sendo uma partícula eletrizada com carga de 12 nC, e a outra com uma carga de 18 nC. Considere a constante eletrostática igual a 9.109 N.m²/c².
16.10⁻5
1,6.10⁻5

8.10⁻5
2,16.10⁻5
Utilizando a lei de Ampere, Calcule aproximadamente o campo magnético no centro de um solenóide de. 0,1m de comprimento, com 600 espiras e percorrido por uma corrente de 2 A. Considere a permeabilidade igual a 
16.10⁻5
1,6.10⁻5
8.10⁻5
2,16.10⁻5